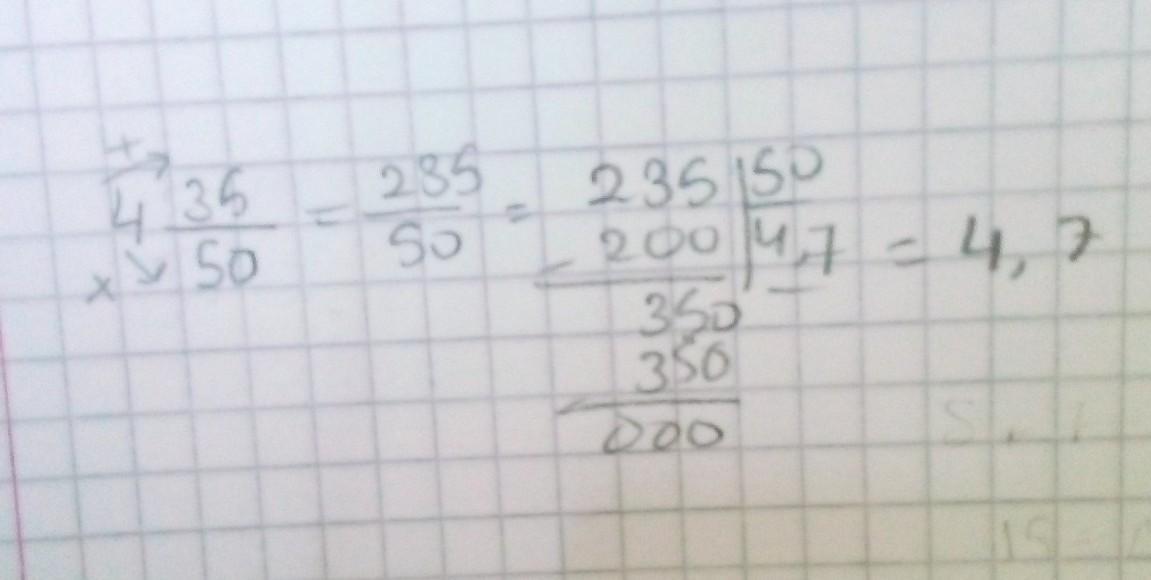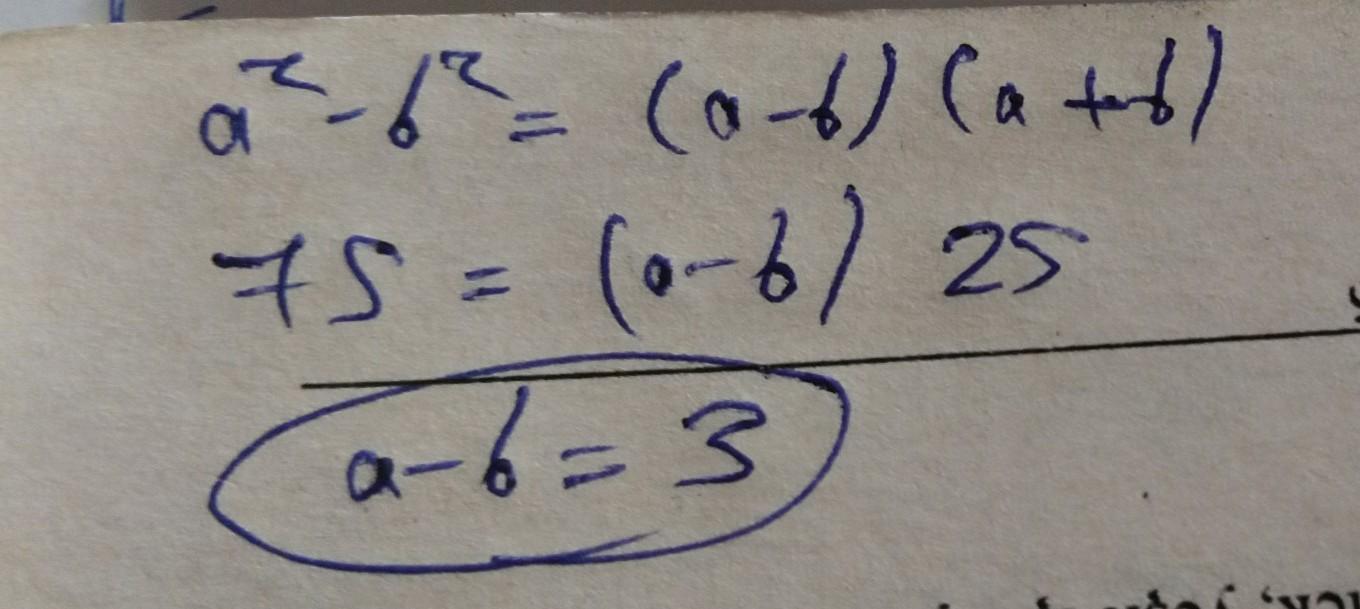Soru: arkadaşlar lütfen DOĞRU CEVABI verin ve boş yorumlar yapmayın lütfen çünkü boş yorum yapanı şikayet ediyorum şimdiden teşekkürler ​

Cevap:

aciklama

Açıklama:

kendine renkli kalemler alabilir renkli not defterleri secebilirsin ayrica calisma masana hedefini veya seni motive edebilecek seyler koyabilir study bunyy indirebilirsin

Cevap:

4,7'dir. İyi dersler. KOLAY GELSİN:)

Cevap:

iyi çalışmalar dilerim

Cevap:

Fonksiyonun Tanımı

A ve B boş olmayan iki küme olsun. A kümesinin her bir elemanını B kümesinin bir ve yalnız bir elemanına eşleyen ilişkiye A dan B ye tanımlı fonksiyon denir. A dan A ya tanımlı bir fonksiyona kısaca A da tanımlı fonksiyon da denir. Fonksiyonlar genellikle f, g, h, F, G, H gibi sembollerle gösterilir.

Bir A kümesinden B kümesine tanımlı f fonksiyonu kısaca şu şekilde gösterilir:

f : A → B

Burada A ya fonksiyonun tanım kümesi, B ye ise fonksiyonun değer kümesi denir.

Eğer f fonksiyonu A kümesinden alınan bir x elemanını, B kümesindeki bir y elemanı ile ilişkilendiriyor ise y, x in f altındaki görüntüsü veya f in x teki değeri y dir denir ve bu durum y = f(x) şeklinde ifade edilir. Tanım kümesindeki elemanların fonksiyon altındaki görüntülerinin oluşturduğu kümeye fonksiyonun görüntü kümesi denir ve f(A) ile gösterilir. Görüntü kümesi ortak özellik yöntemiyle şu şekilde gösterilir:

f(A) = { f(x) : x ∈ A }

Yapmış olduğumuz fonksiyon tanımındaki şu iki özelliği vurgulayalım:

1. Tanım kümesindeki her bir eleman değer kümesinden bir elemanla mutlaka ilişkilendirilmiştir,

2. Tanım kümesindeki herhangi bir eleman değer kümesinden en fazla bir elemanla ilişkilendirilmiştir. ( Bir kişi aynı anda iki farklı şehirde bulunamaz, bir kişinin iki tane öz annesi olmaz, bir kişinin T.C. kimlik numarası bir tanedir.)

Yukarıdaki şartlardan en az biri sağlanmıyorsa f : A → B bir fonksiyon belirtmez.

Örnek

Örnek

Örnek

Örnek

Aşağıda verilen durumların fonksiyon belirtip belirtmeyeceğini bulalım.

a. Alfabedeki her harfin kendisiyle başlayan günle ilişkilendirilmesi

b. Sınıftaki öğrencilerin doğum günleri ile ilişkilendirilmesi

c. Ülkemizdeki vatandaşların Türkiye Cumhuriyeti kimlik numaralarıyla ilişkilendirilmesi

Dikkat edilecek olursa bir fonksiyonun görüntü kümesi, değer kümesinin bir alt kümesidir, yani f(A) ⊂ B dir. Bu durum yandaki gibi bir şekille açıklanabilir.

Örnek

f fonksiyonu x girdisini alıp f(x) çıktısına götüren bir makine şeklinde düşünülebilir.

Başarılar...

Adım adım açıklama:

En iyi seçmeyi unutma :)