Soru: 3 + 6 + 9 + ... + 48 ardışık toplamının sonucu kaçtır? A) 396 B) 399 C) 402 D) 405 E) 408(Nasıl çözdüğünü anlatan ilk ve doğru bulanı en iyi seçeceğim. Lütfen anlatarak yapın)
Cevaplar 1
Merhaba lena
Cevabımız E şıkkıdır.
ardışık sayıların formül olarak bilmen bu kısım ićin denin acindan iyi olacaktir.
Ardışık sayıların toplamı formülü
1 + 2 + 3 +....+ n =n.(n + 1)/2
Ardışık çift sayıların toplamı formülü
2 + 4 + 6 + ... + 2n = n.(n+1)
Ardışık tek sayıların toplamı formülü
1 + 3 + 5 + .... + (2n − 1) = n.n=n2
Ardışık tam kare sayıların toplamı formül
12 + 22 + 32 +....+ n2 =n.(n+1)(2n+1)/6
Ardışık ve küp şeklindeki sayıların toplamları formülü
13 + 23 + 33 +....+ n3 = [n.(n + 1)2]2
Ardışık ve 4. dereceli sayıların toplamı formülü
14 + 24 + 34 +....+ n4 =n.(n+1)(2n+1)(3n²+3n+1)6
Terim sayısını veren formül
Terim Sayısı= [büyük terim - küçük terimartışmiktarı] +1
-
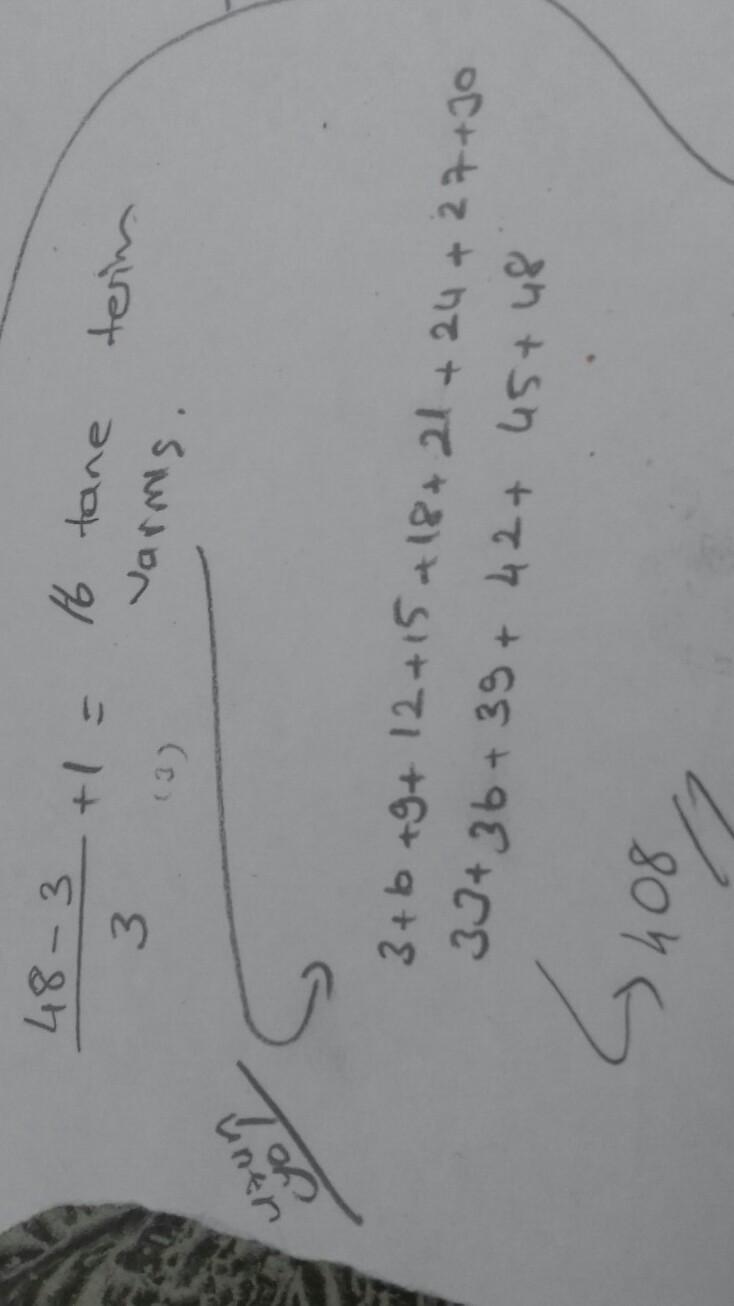
Yazar:
rishif5eo
-
Bir cevabı oylayın:
12
Cevabı biliyor musunuz? Buraya ekleyin!
Size yardımcı olabilecek diğer ilgili sorular
-
Yazar:
orestes
-
Yazar:
ezequielfernandez
-
Bir cevabı oylayın:
0
-
Yazar:
bernardo
-
Yazar:
onésimotgqk
-
Bir cevabı oylayın:
8
-
Yazar:
adanqsk8
-
Bir cevabı oylayın:
12
-
Yazar:
winston35
-
Yazar:
oseasj0ql
-
Bir cevabı oylayın:
10
-
Yazar:
hulk
-
Yazar:
harriettmqg
-
Bir cevabı oylayın:
7
-
Yazar:
sassytdiu
-
Bir cevabı oylayın:
0